
Fibonacci
sequence
By
Princess Browne
Generate a
Fibonacci sequence in the first column using f (0) = 1, f (1) = 1,
F (n) = f (n-1) + f (n-2)
a.
Construct
the ratio of each pair of adjacent terms in the Fibonacci sequence. What
happens as n increases? What about the ratio of every second term? etc.
b.
Explore sequences where f (0) and f (1)
are some arbitrary integers other than 1. If f (0) =1 and f (1) = 3, then your
sequence is a Lucas Sequence. All such sequences, however, have the same limit
of the ratio of successive terms.
The
Fibonacci numbers are a sequence of numbers named after Leonardo of Pisa, who
was also known as Fibonacci.
The
following relation defines the Fibonacci sequence:
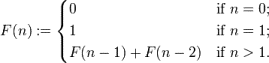
The following spreadsheet will use the formula of f (n) =
f (n-1) + f (n -2) to show the value of the Golden Ratio.
Formula: Xn = F (n=1)/ F (n) = F (n)
+ F (n-1)/ F (n) = 1 + F (n-1)/F (n) = 1 + 1/ (F (n)/F (n-1)) = 1 + 1/Xn -
1
|
1 |
|
|
|
|
|
1 |
1 |
|
|
|
|
2 |
2 |
2 |
|
|
|
3 |
1.5 |
3 |
3 |
|
|
5 |
1.666666667 |
2.5 |
5 |
5 |
|
8 |
1.6 |
2.666666667 |
4 |
8 |
|
13 |
1.625 |
2.6 |
4.333333333 |
6.5 |
|
21 |
1.615384615 |
2.625 |
4.2 |
7 |
|
34 |
1.619047619 |
2.615384615 |
4.25 |
6.8 |
|
55 |
1.617647059 |
2.619047619 |
4.230769231 |
6.875 |
|
89 |
1.618181818 |
2.617647059 |
4.238095238 |
6.846153846 |
|
144 |
1.617977528 |
2.618181818 |
4.235294118 |
6.857142857 |
|
233 |
1.618055556 |
2.617977528 |
4.236363636 |
6.852941176 |
|
377 |
1.618025751 |
2.618055556 |
4.235955056 |
6.854545455 |
|
610 |
1.618037135 |
2.618025751 |
4.236111111 |
6.853932584 |
|
987 |
1.618032787 |
2.618037135 |
4.236051502 |
6.854166667 |
|
1597 |
1.618034448 |
2.618032787 |
4.236074271 |
6.854077253 |
|
2584 |
1.618033813 |
2.618034448 |
4.236065574 |
6.854111406 |
|
4181 |
1.618034056 |
2.618033813 |
4.236068896 |
6.854098361 |
|
6765 |
1.618033963 |
2.618034056 |
4.236067627 |
6.854103343 |
|
10946 |
1.618033999 |
2.618033963 |
4.236068111 |
6.85410144 |
|
17711 |
1.618033985 |
2.618033999 |
4.236067926 |
6.854102167 |
|
28657 |
1.61803399 |
2.618033985 |
4.236067997 |
6.85410189 |
|
46368 |
1.618033988 |
2.61803399 |
4.23606797 |
6.854101996 |
|
75025 |
1.618033989 |
2.618033988 |
4.23606798 |
6.854101955 |
|
121393 |
1.618033989 |
2.618033989 |
4.236067976 |
6.854101971 |
|
196418 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101965 |
|
317811 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101967 |
|
514229 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
|
832040 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
|
1346269 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
|
2178309 |
1.618033989 |
2.618033989 |
4.236067977 |
6.854101966 |
|
3524578 |
1.618033989 |
2.618033989 |
4.236067978 |
6.854101966 |
|
|
|
|
|
|
From the table, we will see that the first column is the
value of n, the second column give us the value of the golden ratio (1.61), the
third column gives us the square of golden ratio (2.618), and the fourth column
gives us the cube of the golden
ratio (4.23) and so on.
Next, we want to see the table when f (0) and f (1) are
some arbitrary integers other than 1. If f (0) =1 and f (1) = 3, then our
sequence is a Lucas Sequence. All such sequences have the same limit of the
ratio of successive terms.
|
3 |
3 |
|
|
|
|
4 |
4 |
4 |
|
|
|
7 |
7 |
2.333333 |
7 |
|
|
11 |
11 |
2.75 |
3.666667 |
11 |
|
18 |
18 |
2.571429 |
4.5 |
6 |
|
29 |
29 |
2.636364 |
4.142857 |
7.25 |
|
47 |
47 |
2.611111 |
4.272727 |
6.714286 |
|
76 |
76 |
2.62069 |
4.222222 |
6.909091 |
|
123 |
123 |
2.617021 |
4.241379 |
6.833333 |
|
199 |
199 |
2.618421 |
4.234043 |
6.862069 |
|
322 |
322 |
2.617886 |
4.236842 |
6.851064 |
|
521 |
521 |
2.61809 |
4.235772 |
6.855263 |
|
843 |
843 |
2.618012 |
4.236181 |
6.853659 |
|
1364 |
1364 |
2.618042 |
4.236025 |
6.854271 |
|
2207 |
2207 |
2.618031 |
4.236084 |
6.854037 |
|
3571 |
3571 |
2.618035 |
4.236062 |
6.854127 |
|
5778 |
5778 |
2.618034 |
4.23607 |
6.854093 |
|
9349 |
9349 |
2.618034 |
4.236067 |
6.854106 |
|
15127 |
15127 |
2.618034 |
4.236068 |
6.854101 |
|
24476 |
24476 |
2.618034 |
4.236068 |
6.854102 |
|
39603 |
39603 |
2.618034 |
4.236068 |
6.854102 |
|
64079 |
64079 |
2.618034 |
4.236068 |
6.854102 |
|
103682 |
103682 |
2.618034 |
4.236068 |
6.854102 |
|
167761 |
167761 |
2.618034 |
4.236068 |
6.854102 |
|
271443 |
271443 |
2.618034 |
4.236068 |
6.854102 |
|
439204 |
439204 |
2.618034 |
4.236068 |
6.854102 |
|
710647 |
710647 |
2.618034 |
4.236068 |
6.854102 |
|
1149851 |
1149851 |
2.618034 |
4.236068 |
6.854102 |
|
1860498 |
1860498 |
2.618034 |
4.236068 |
6.854102 |
|
1 |
|
|
|
|
|
5 |
5 |
|
|
|
|
6 |
1.2 |
6 |
|
|
|
11 |
1.833333333 |
2.2 |
11 |
17 |
|
17 |
1.545454545 |
2.833333333 |
3.4 |
5.6 |
|
28 |
1.647058824 |
2.545454545 |
4.666666667 |
7.5 |
|
45 |
1.607142857 |
2.647058824 |
4.090909091 |
6.636363636 |
|
73 |
1.622222222 |
2.607142857 |
4.294117647 |
6.941176471 |
|
118 |
1.616438356 |
2.622222222 |
4.214285714 |
6.821428571 |
|
191 |
1.618644068 |
2.616438356 |
4.244444444 |
6.866666667 |
|
309 |
1.617801047 |
2.618644068 |
4.232876712 |
6.849315068 |
|
500 |
1.618122977 |
2.617801047 |
4.237288136 |
6.855932203 |
|
809 |
1.618 |
2.618122977 |
4.235602094 |
6.853403141 |
|
1309 |
1.618046972 |
2.618 |
4.236245955 |
6.854368932 |
|
2118 |
1.61802903 |
2.618046972 |
4.236 |
6.854 |
|
3427 |
1.618035883 |
2.61802903 |
4.236093943 |
6.854140915 |
|
5545 |
1.618033265 |
2.618035883 |
4.23605806 |
6.854087089 |
|
8972 |
1.618034265 |
2.618033265 |
4.236071766 |
6.854107649 |
|
14517 |
1.618033883 |
2.618034265 |
4.23606653 |
6.854099796 |
|
23489 |
1.618034029 |
2.618033883 |
4.23606853 |
6.854102795 |
|
38006 |
1.618033973 |
2.618034029 |
4.236067766 |
6.85410165 |
|
61495 |
1.618033995 |
2.618033973 |
4.236068058 |
6.854102087 |
|
99501 |
1.618033987 |
2.618033995 |
4.236067947 |
6.85410192 |
|
160996 |
1.61803399 |
2.618033987 |
4.236067989 |
6.854101984 |
|
260497 |
1.618033988 |
2.61803399 |
4.236067973 |
6.85410196 |
|
421493 |
1.618033989 |
2.618033988 |
4.236067979 |
6.854101969 |
|
681990 |
1.618033989 |
2.618033989 |
4.236067977 |
0 |
As
n increases,
f
(n+1)/f (n) = 1.618, f (n+2) / f (n) = 2.618, f (n +3) / f (n) =4.236, and f (n
+4)/ f (n) = 6.854 and so fourth.
From
the tables, we can see that the value of n does not determine the outcome of
the table/sequences. I find it interesting how the fifth column of the last
graph ends up being zero, as n increases the graph will generate a value for
this column.